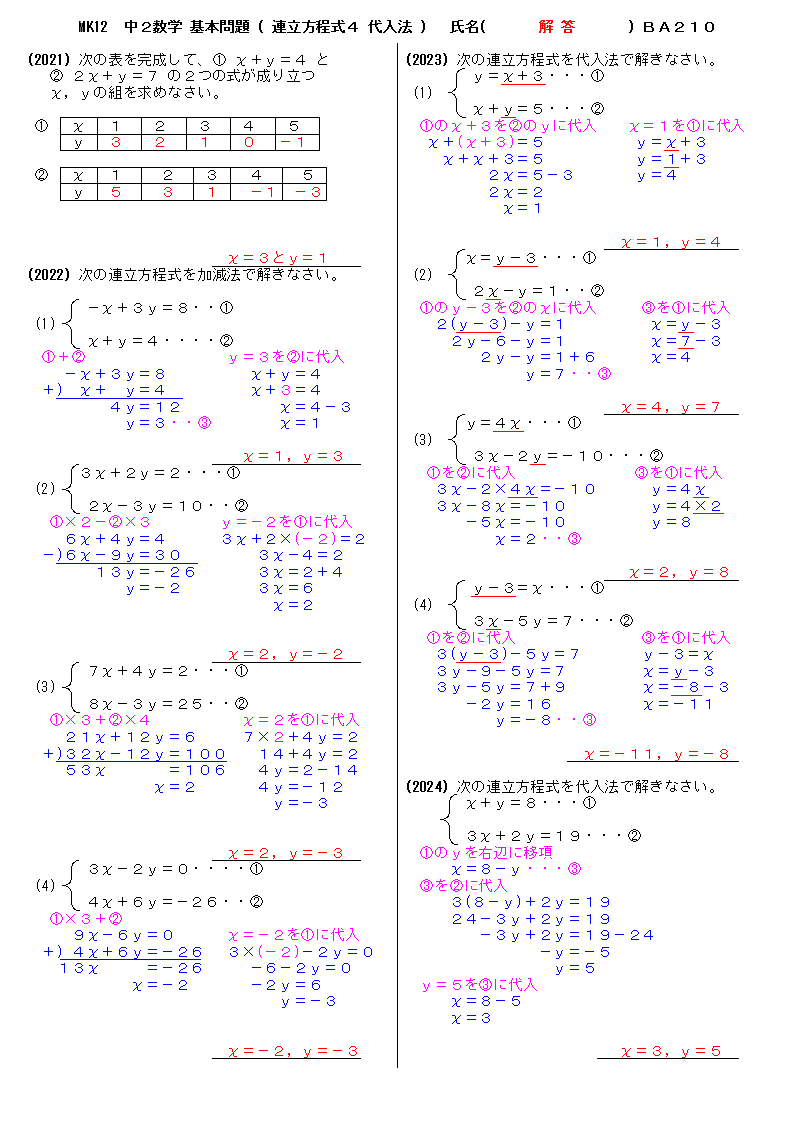
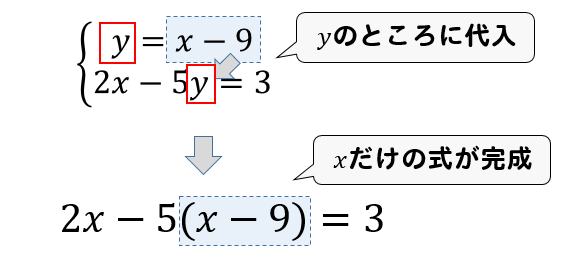
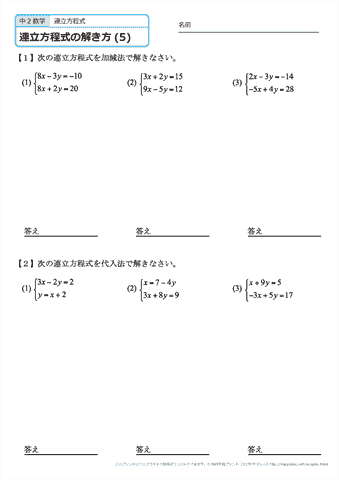
※加減法でもできますが、ここでは代入法で行った場合の答案を示しています。 問21 次の連立方程式を解きなさい。 (空欄を埋めて答案を完成しなさい。
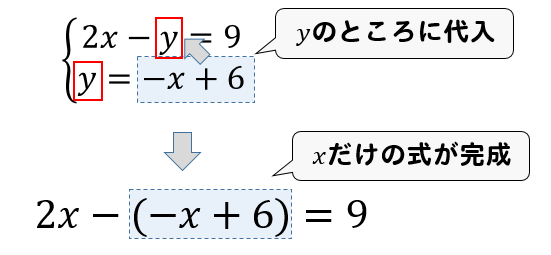
連立方程式 代入法- ガウスの消去法の概要 ガウスの消去法は 前進消去 (文字を1つずつ消していく操作)と 後退代入 (1成分ずつ答えを求めていく操作)からなります。 順々に説明していきます。 注:以下では方程式の数と変数の数が同じで,解が一つしかない(係数行列が正則)場合を考えます。連立方程式の解き方 では連立方程式を実際に解いてみましょう。 先程例に挙げた を使って考えていきます。 解き方は様々ですが、ここでは代入法という方法を使って解いていきます。 ①か②を「x=」もしくは「y=」の形に変形する。 今回は②
連立方程式 代入法のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 | ||
 |  |  |
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 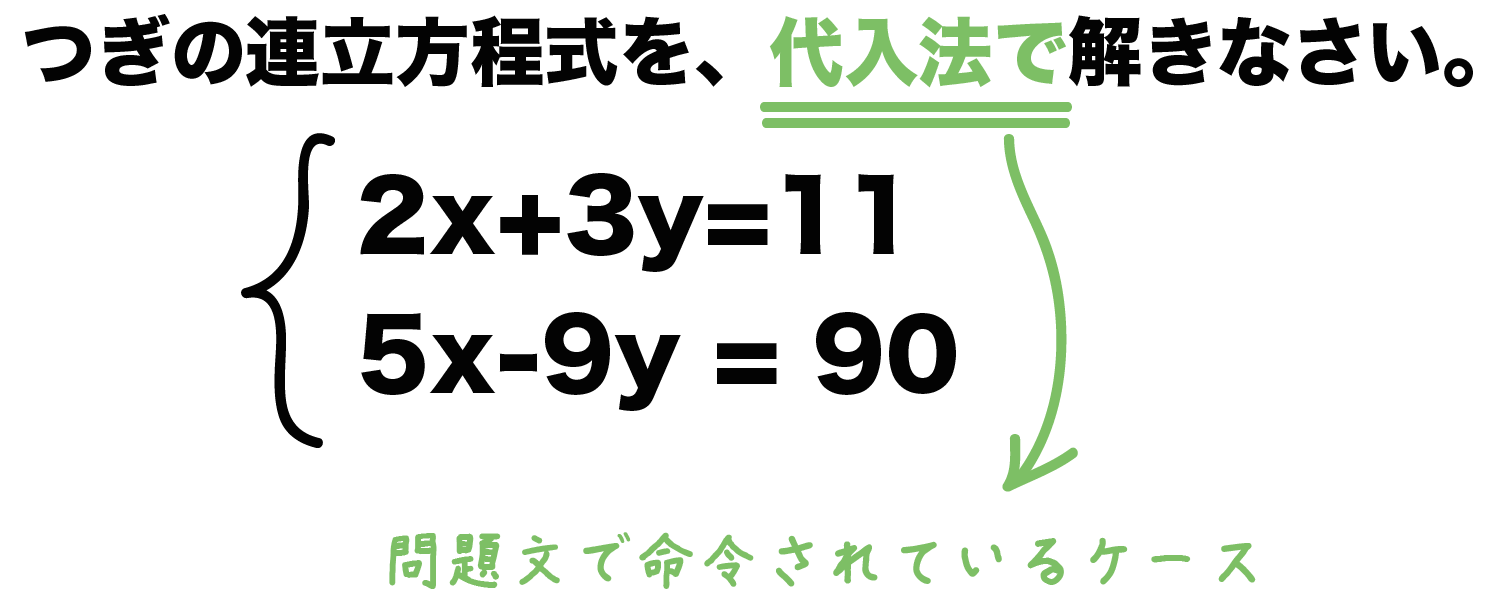 | |
 | ||
 |  | |
 |  | 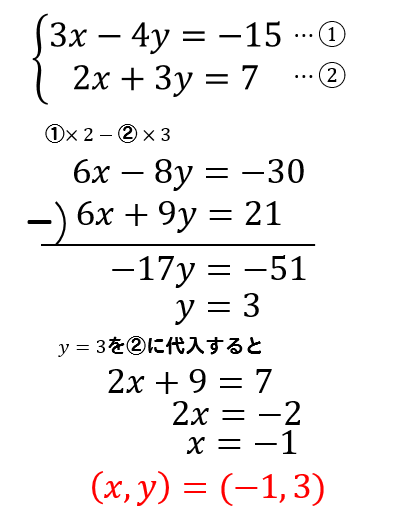 |
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 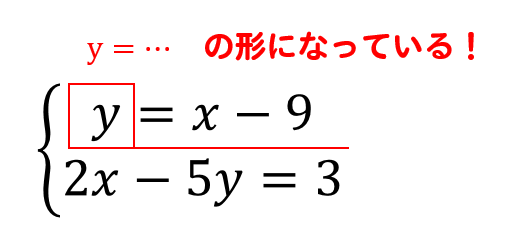 |
 |  | |
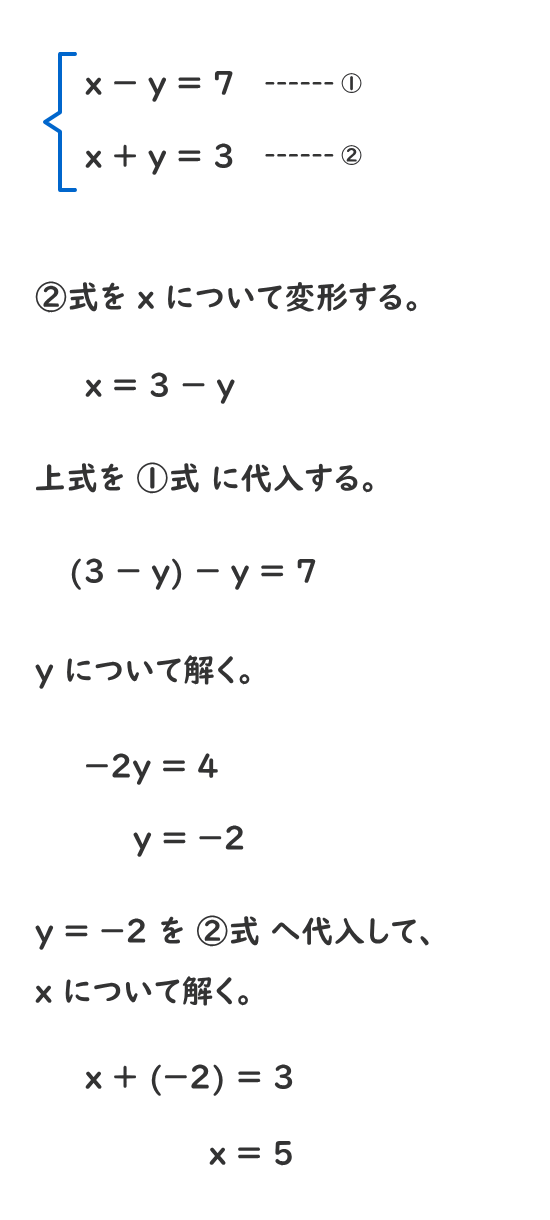 | ||
 |  | |
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
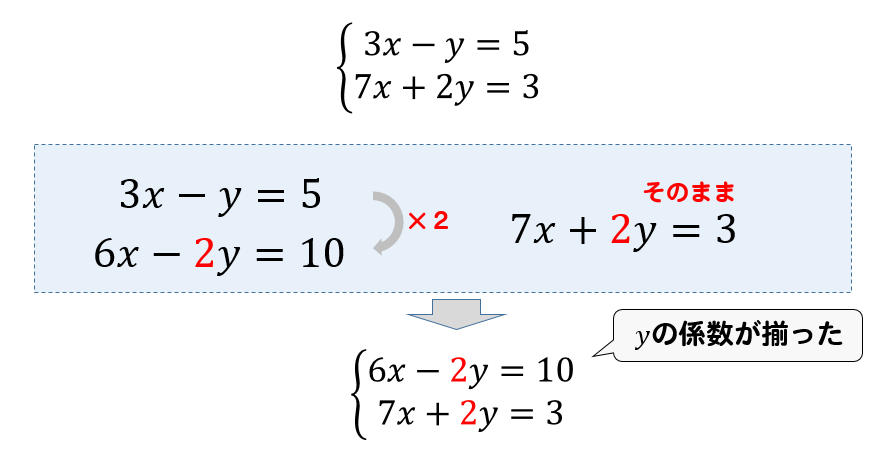 |  |  |
 |  | |
 |  |  |
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 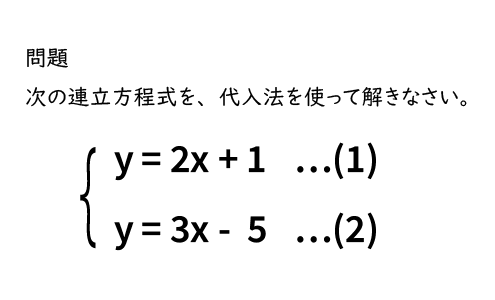 |  |
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
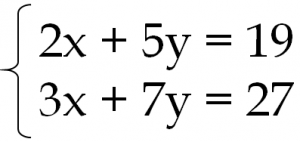 |  | |
 |  | |
 |  | |
 | ||
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 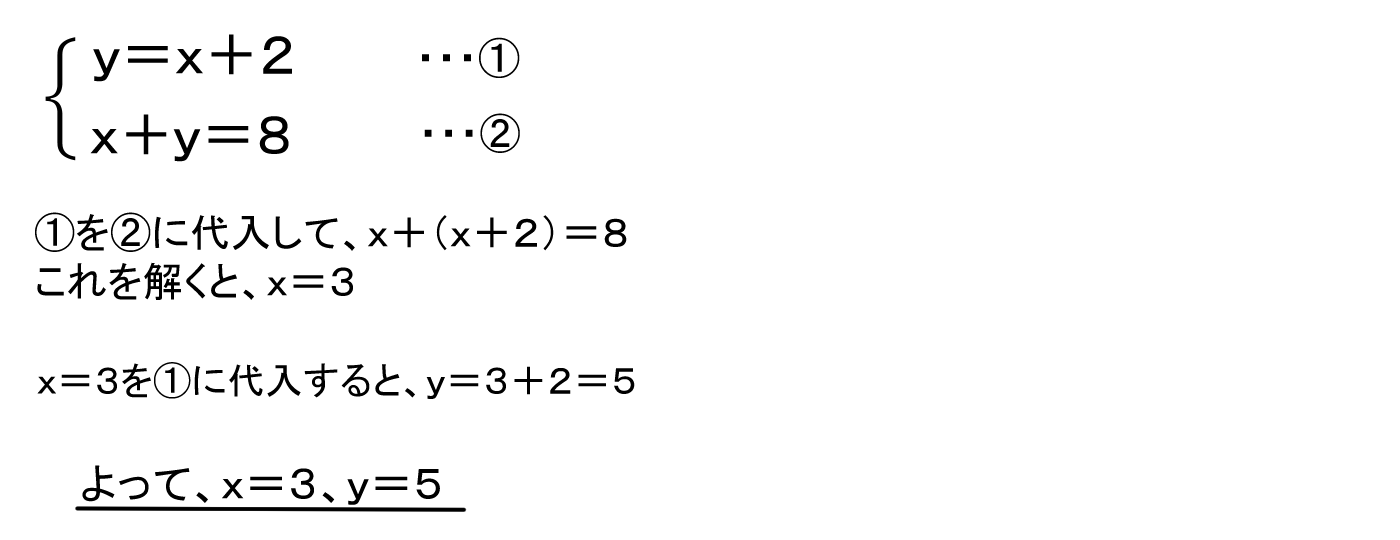 |  |
 | 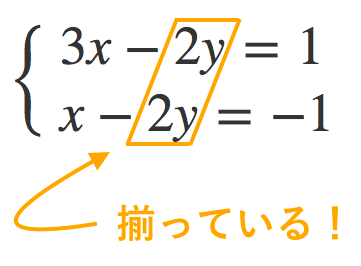 |  |
 |  | 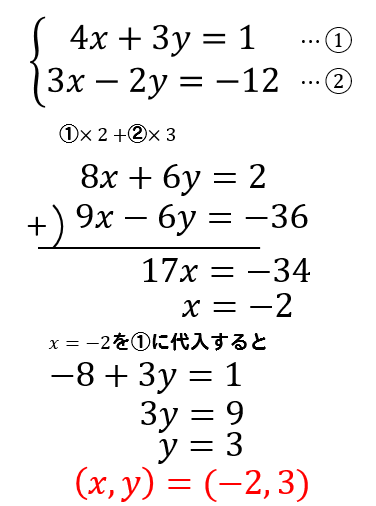 |
 |  | |
「連立方程式 代入法」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
連立1次方程式を代入法で計算するポイントの通りに計算すると、x=10という答えが出ました。 ここまで計算すれば後は簡単です。 次は、このx=10を式(1)か式(2)に代入してyの値を計算します。 式を見ると式(2)の方が簡単そうに思いますので式(2)に代入します。 代入すると10+y=5と 連立方程式の解き方基本:代入法 さて、加減法の次は代入法です。 代入法とは、「方程式を他の方程式にはめこむこと」。こちらも例題を用いて詳しく説明します。 問題xとyの値を求めよ。 2xy=1 x2y=8 (加減法の説明で用いた例題と同じ問題です) 解説 まず、説明がしやす





0 件のコメント:
コメントを投稿